はじめに
どーも、ふぁんぼです。
毎度ご覧いただきありがとうございます。
今回は初級プログラム4で板を立てる動作の「角付け」についての解説になります。
初級プログラム各回、順を追っての解説になっており、前回までの知識が必要になる場合が多いです。これまでの記事も併せてご覧いただければ幸いです。
【初級プログラム2】
カービングターンをするために、まずは板をどうすればよいか理解しよう!
【初級プログラム3】
安定した角付けのポジションとは
前々回の初級プログラム2で、カービングターンは板を立ててサイドカーブを使った曲がり方(曲線運動)がメインになるとご説明しました。
この板を立てる動作を「角付け」といいますが、前述した通りカービングターンでは板を立てての曲がり方がメインになるので、人間はこの角付けを積極的に行う必要がありカービンクでは重要なボード操作の1つになります。
この角付け行うにあたり、力学的に安定した状態を理解しておくことがカービングターンを習得する上でとても重要になってきます。
さて、最初に結論から申し上げておきますね。
安定した角付けのポジションとは、
角付け中の板に作用する重力方向と遠心力方向それぞれのモーメントが釣り合っている状態
です。

さらに別の言い方をすれば、
重力と遠心力の合力の作用線が接雪してるエッジを通る状態
です。

2つの言い方をしましたが、まとめて申し上げると、
重力方向と遠心力方向のモーメントが釣り合うとき、合力の作用線は接雪しているエッジを必ず通る
ということです。
そしてこの条件を満たすには、上の画像からイメージできるように重心の位置がとても重要になります。
※重心の位置次第では合力の作用線は接雪しているエッジを通らない
さて、合力とかモーメントとか物理嫌いの方には頭が痛い話ですが、スノーボード上達には絶対に必要な知識になります。
できるだけわかりやすく、以下のポイントに分けて解説していきますので、是非最後までお付き合いいただければと思います。
【今回のポイント】
1.ターン中、主に作用する力は重力と遠心力とその合力
2.ターン中に作用する力に関連しモーメントが発生する
3.モーメントのコントロールは重心位置のコントロール
ターン中、主に作用する力は重力遠心力とその合力
ポイント1についての解説です
地球にいれば人間には常に鉛直方向に重力が作用しています。
※厳密には同時に垂直抗力も作用します

ターン中ともなれば、そこに遠心力が働きます。
もちろんそれぞれの力が作用する場所は、人間の重心です。
※厳密にはスノーボードと人間の合成重心です
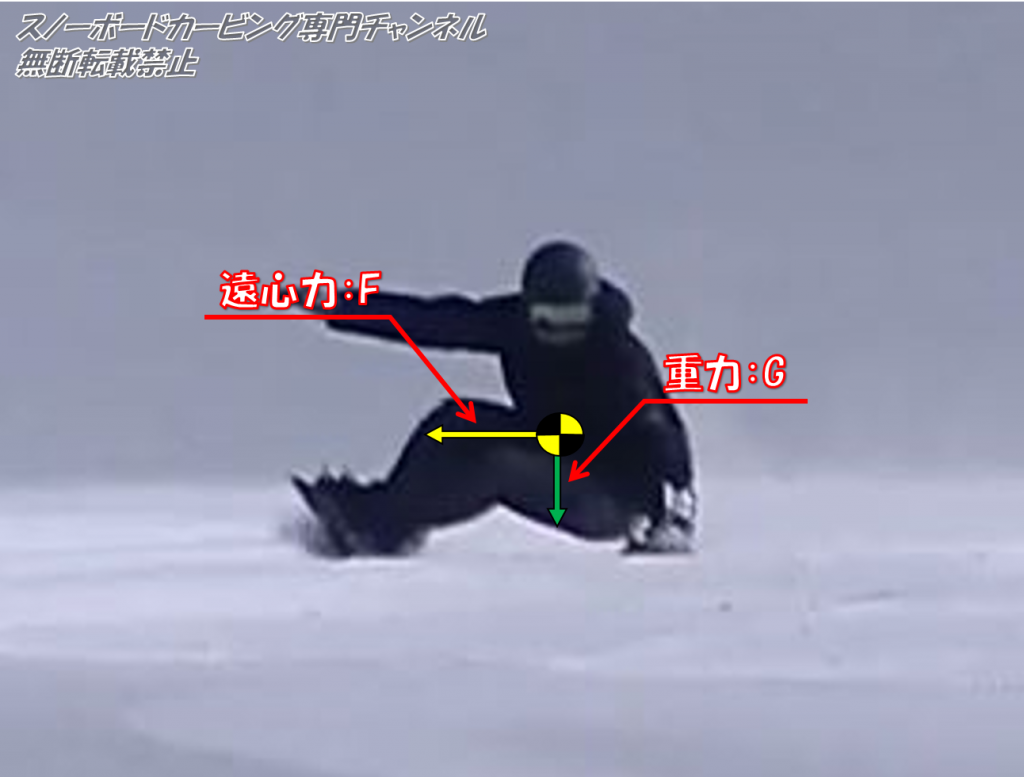
これらの力は地球上にいる限り万物平等のルールみたいなもので避けられない力なので機械的に理解して下さい。
さてターン中は主に重力と遠心力2つの力が人間に働くわけですが、同じ物体に複数の力が働いているときは、それらの力が合成して働くことになります。
こちらの映像をご覧下さい。(2:57~3:09)
見ていただいたように力の合成方向に板の模型が動きました。
同じ理屈でターン中は重力と遠心力が働くと同時に、それぞれの力を合成した合力が働くことになります。
ちょうどこちらの画像のような状態です。
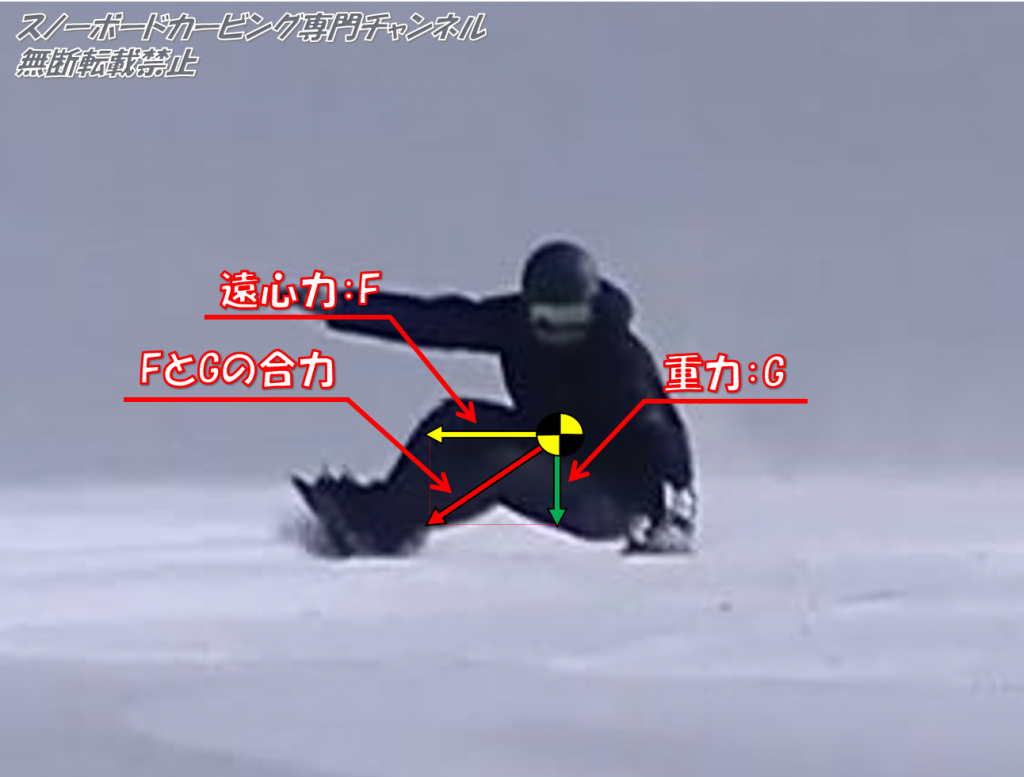
ターン中、主に作用する力は重力と遠心力とその合力
ちなみに先の結論で申し上げてましたが、この合力の作用線が接雪しているエッジを通る状態が力学に安定した角付けのポジションになります。(詳細はポイント3で解説します)
ターン中に作用する力に関連しモーメントが発生する
続いてポイント2の解説になります。
ターン中は先程説明した力に関連してモーメントが発生します。
モーメントとは単純にいうと物体を回転させようとする力ですが、モーメントに馴染みの無い方向けに少し解説したいと思います。
ボルトを回すときに長いスパナを使うとラクに回せるように、物体を回転させるには力だけでなく、物体の回転軸から力をかける場所までの距離も影響します。
単純な力だけではなく、その距離を含めた回転させようとする作用の量をモーメントといい、このモーメントは「回転軸から力をかける場所までの距離」と「その力」の積で決まります。
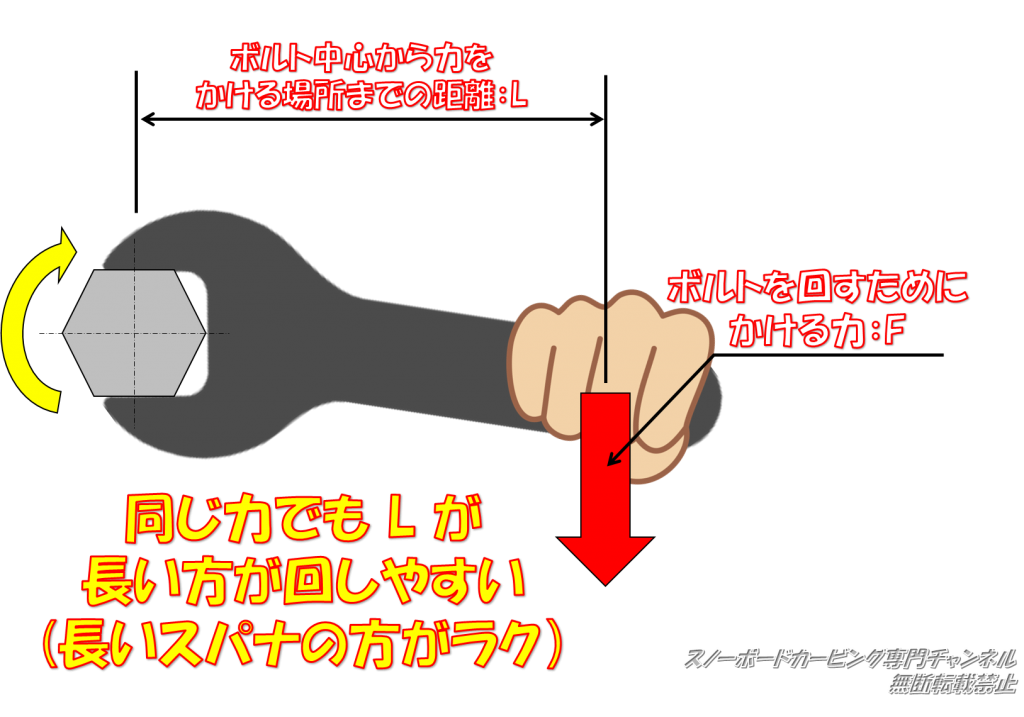
上の図でボルトにかかるモーメントをMとすると、そのモーメントは
M = F × L
となります。
計算式より、Lが長ければ長いほどモーメントが大きくなり回転させようとする作用も大きくなるので、長いスパナはボルトがラクに回せるのが理解できますね。
実はこのモーメントですが、重力と遠心力に関連しターン中(角付け中)の板に下の画像のように作用することになります。
※力は同一作用線上であればスライドして考えることができます
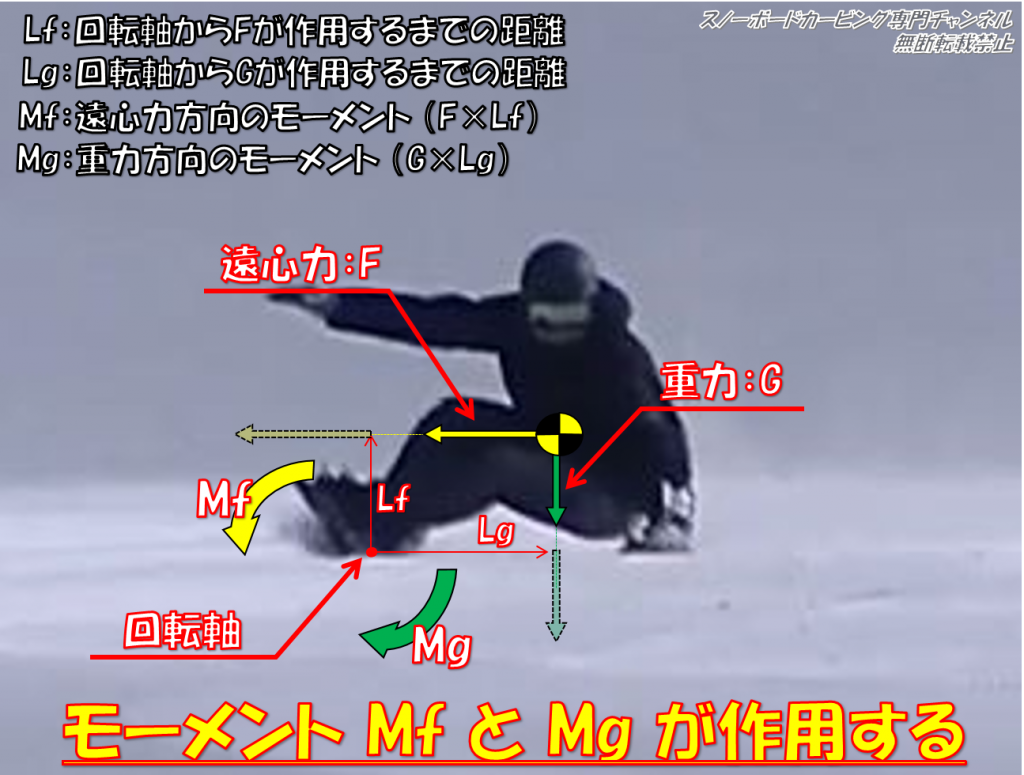
ターン中に作用する力に関連しモーメントが発生する
ちなみにターンしようとした際、無意識かつ直感的に自分が傾いてると思いますがそれはなぜでしょうか?
答えは上の画像のように接雪しているエッジが回転軸となって、重力方向と遠心力方向にそれぞれモーメントが発生するため、それらのモーメントの均衡をとろうと無意識に重心をターン内側に移動しようとするためです。
ちなみに冒頭の結論で申し上げてましたが、このそれぞれのモーメントが釣り合っている状態が安定した角付けのポジションです。
詳細は次のポイント3で解説しますが、仮にどちらかのモーメントが強い場合、板の傾きを維持していた均衡が崩れ転倒リスクが生じるのがイメージできると思います。
モーメントのコントロールは重心位置のコントロール
続いてはポイント3の解説です。
先程のポイント2でターン中(角付け中)の板に重力方向と遠心力方向にモーメントが発生すると申し上げました。
この2つのモーメントの方向は相反するものなので、この2つのバランスがとれていれば板はその傾きを維持し安定した状態でターンができます。
逆にどちらか一方のモーメントが強ければ、板の傾きを維持していた均衡が崩れ、板はモーメントが強い方に回転しようとするので転倒のリスクにつながります。
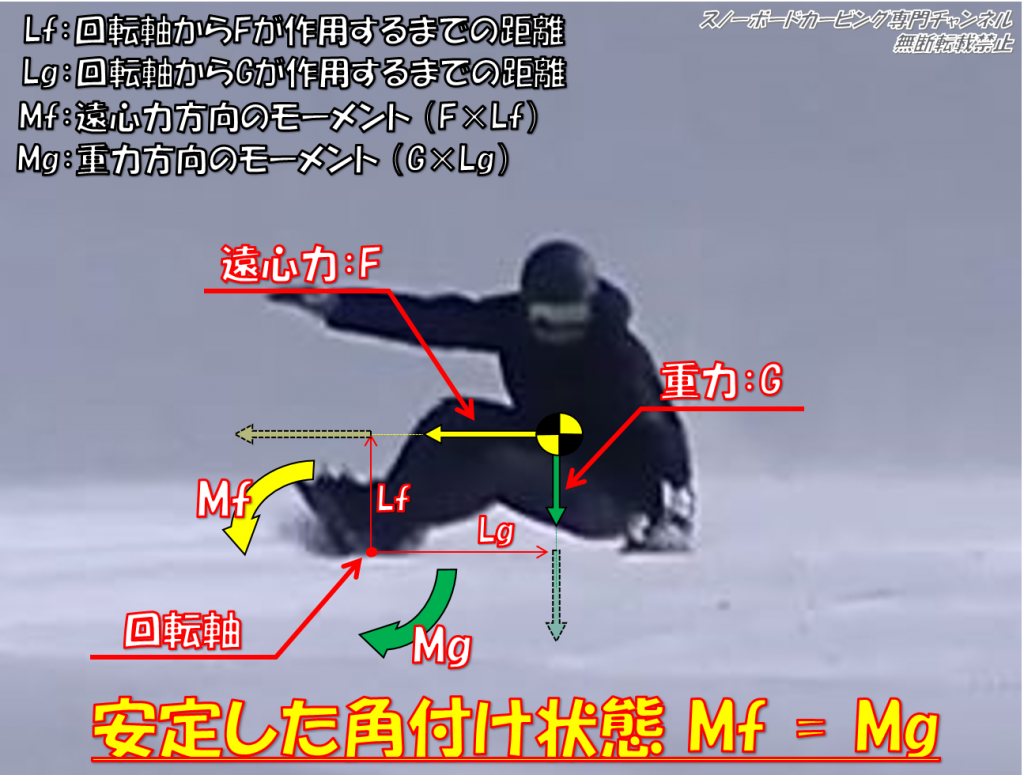
ここで下の画像の状態をそれぞれのモーメントが釣り合っている状態とし、関連する要素を記してある通りに定義したとき、
Mf = Mg つまり F × Lf = G × Lg
となります。
今度はこの局面からモーメントが釣り合っていない不安定な状態を擬似的に考えてみます。
下の画像のように重心の位置をわずかにずらしてみます。
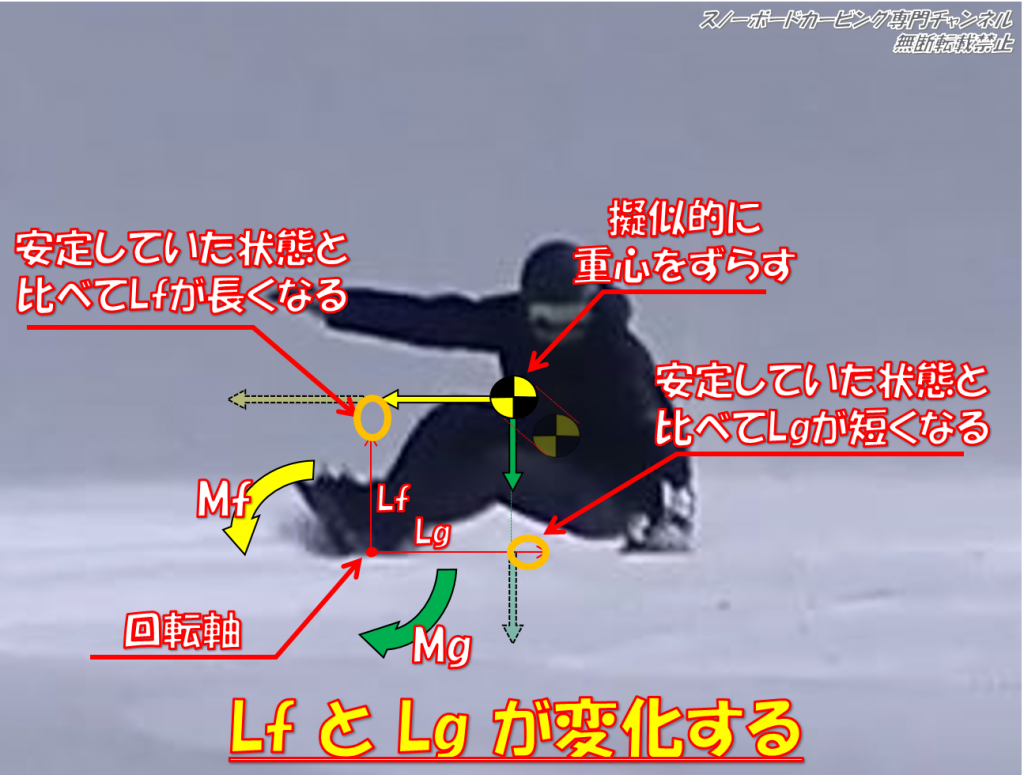
このときの状態として、先程と同じターン局面なので作用している重力と遠心力は同じですが、重心位置の変化に伴い回転軸からそれぞれの力が作用するまでの距離(LfとLg)が変わるのがわかります。
変化した後の距離をそれぞれ Lf ‘ と Lg ‘ としたとき Lf < Lf ‘ 、Lg > Lg ‘ となります。
また、それに伴うモーメントを Mf ‘ と Mg ‘ としたとき下の画像のように
Mf ‘ > Mg ‘ つまり F × Lf ‘ > G × Lg ‘
となります。
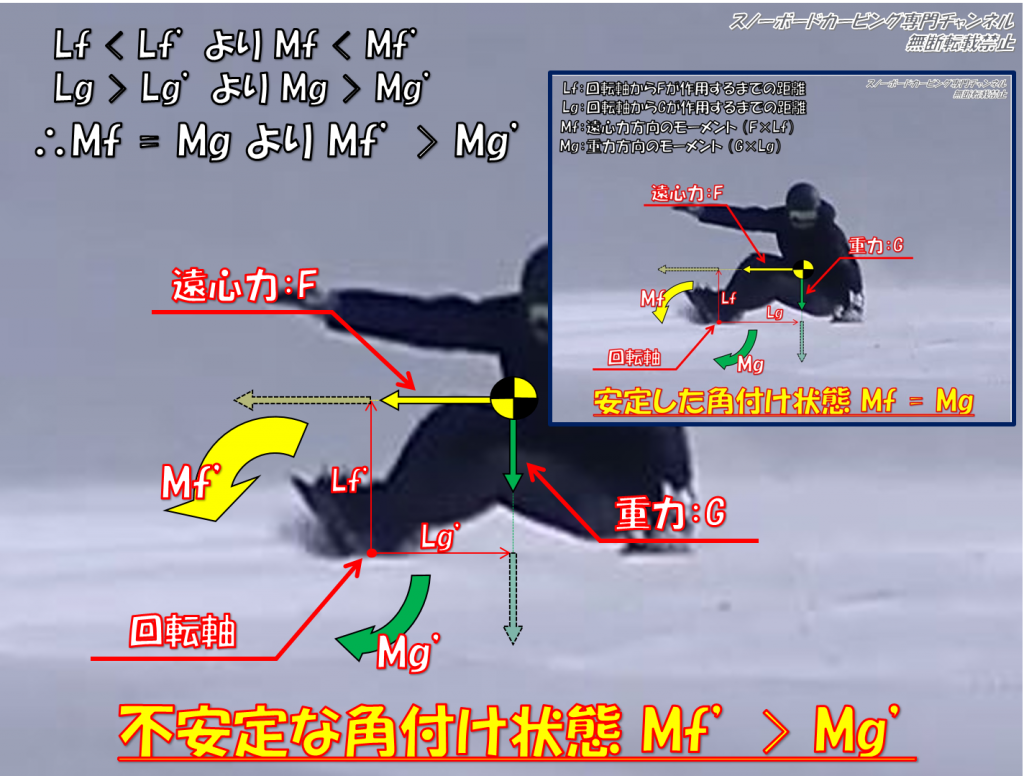
上の画像は遠心力方向のモーメントが重力方向のモーメントより大きい状態です。
この状態ではモーメントの釣り合いがくずれ、板が遠心力方向へ回転する力がかかり不安定な状態となります。
仮に、この状態で遠心力方向へのモーメント Mf ‘ に耐えられなくなった場合、逆エッジでの転倒につながります。
今ご説明した安定した状態と不安定な状態の違いを生んだのはなんだったでしょうか?
ズバリ、重心の位置でしたね。
角付けの基本はそれぞれのモーメントの均衡が取れる位置に重心を置き続けることで、それが力学的に安定した角付けのポジションになります。
モーメントのコントロールは重心位置のコントロール
さて、解説のために重力と遠心力それぞれのモーメントを考えましたが、実は合力のモーメント1つだけを考えた方が簡単だったりしますw
重力と遠心力の合力の作用線が、接雪するエッジを通れば角付け中の板にモーメントは発生しません。
この状態は必然的に重力と遠心力のモーメントが必然的に釣り合う状態になるのです。
下の画像を見比べていただければイメージしていただけると思います。
※力がかかる場所が回転軸からのゼロではモーメントは発生しません
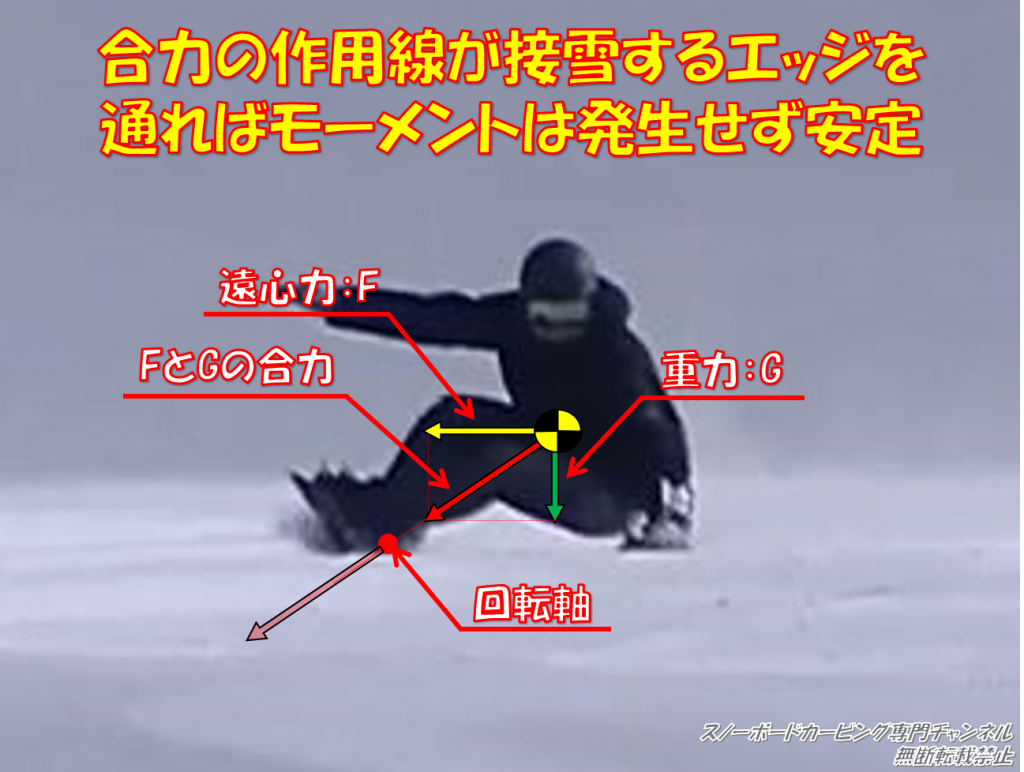
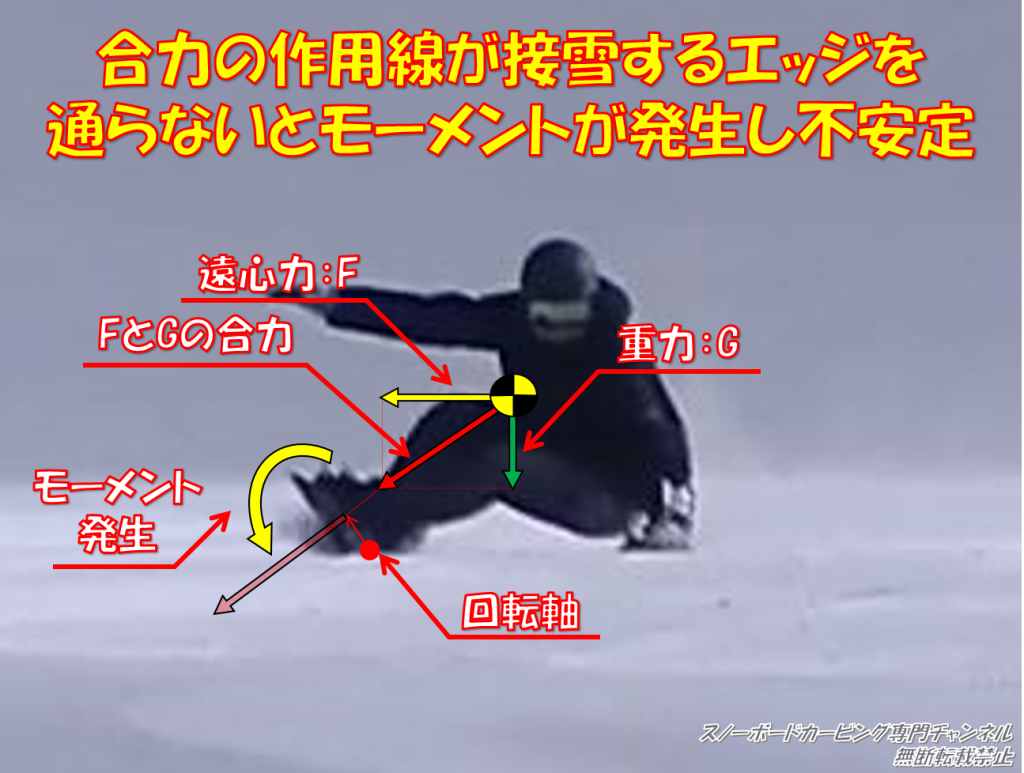
重力方向と遠心力方向のモーメントが釣り合うとき、合力の作用線は接雪しているエッジを必ず通る
まとめ
以下のように各ポイントにわけ解説させていただきました。
【今回のポイント】
1.ターン中、主に作用する力は重力と遠心力とその合力
2.ターン中に作用する力に関連しモーメントが発生する
3.モーメントのコントロールは重心位置のコントロール
ここで改めて結論です。
安定した角付けのポジションとは、
角付け中の板に作用する重力方向と遠心力方向それぞれのモーメントが釣り合っている状態
||
重力と遠心力の合力の作用線が接雪してるエッジを通る状態
です。そしてそのために、
それぞれのモーメントが釣り合うように角付け中は常に重心位置のコントロールが必要
になります。
ちなみに重力と遠心力は以下の公式で求められます。
重力 = m × g (N) 遠心力 = m × v^2 / r (N)
m:自分の質量 (kg) g:重力加速度(9.8m/s^2) v:速度 (m/s) r:回転半径 (m)
今回の解説にあたり、ターン中(角付け中)のある局面(任意の一瞬)を例に解説させていただきましたが、 実際のターンは連続したもので、その局面局面で回転半径やスピードは変化し続けます。
上記の公式より、回転半径やスピードが変化がすれば遠心力も同様に変化し続けるのが分かります。
※重力は常に一定です
当然ですが、遠心力が変化すればその遠心力方向のモーメントも変化します。
ですので、現実のターン(角付け)では変化し続ける遠心力にあわせ、重心位置をモーメントが釣り合うように常にコントロールし続ける必要があるのです。
ターン中、倒れそうになったり吹っ飛びそうなったりすることがあれば、その原因のほとんどはモーメントが釣り合う位置に重心がないからです。
これ機に「角付け = モーメントが釣り合う位置への連続した重心移動」と理解していただき上達に役立てていただければ幸いです。
補足
下の画像のようにモーメントのバランスがくずれたからといって即転倒するわけではありません。

人間には筋力があるのである程度耐えらます。
そしてターン終了時、次のターンに切り替える時の板の動きを考えたとき、あえて上の画像のように遠心力方向のモーメントを発生させないといけないのが想像できると思います。
ターン中は、モーメントが釣り合う位置に重心を移動し続けるのが基本と申し上げてましたが、切り替えではあえてそのバランスを崩すことが必要になります。
その際、重心位置のコントロール次第で意図的に強い遠心力方向のモーメントを発生させることもでき、素早い切り替えに応用することも可能です。
おいおい解説したいとは思いますが、上級者向けのテクニックなのでここではそんなこともできるんだ程度に覚えていただければと思います。
それでは最後までお付き合いありがとうございました。
よりよいスノーボードライフを!
